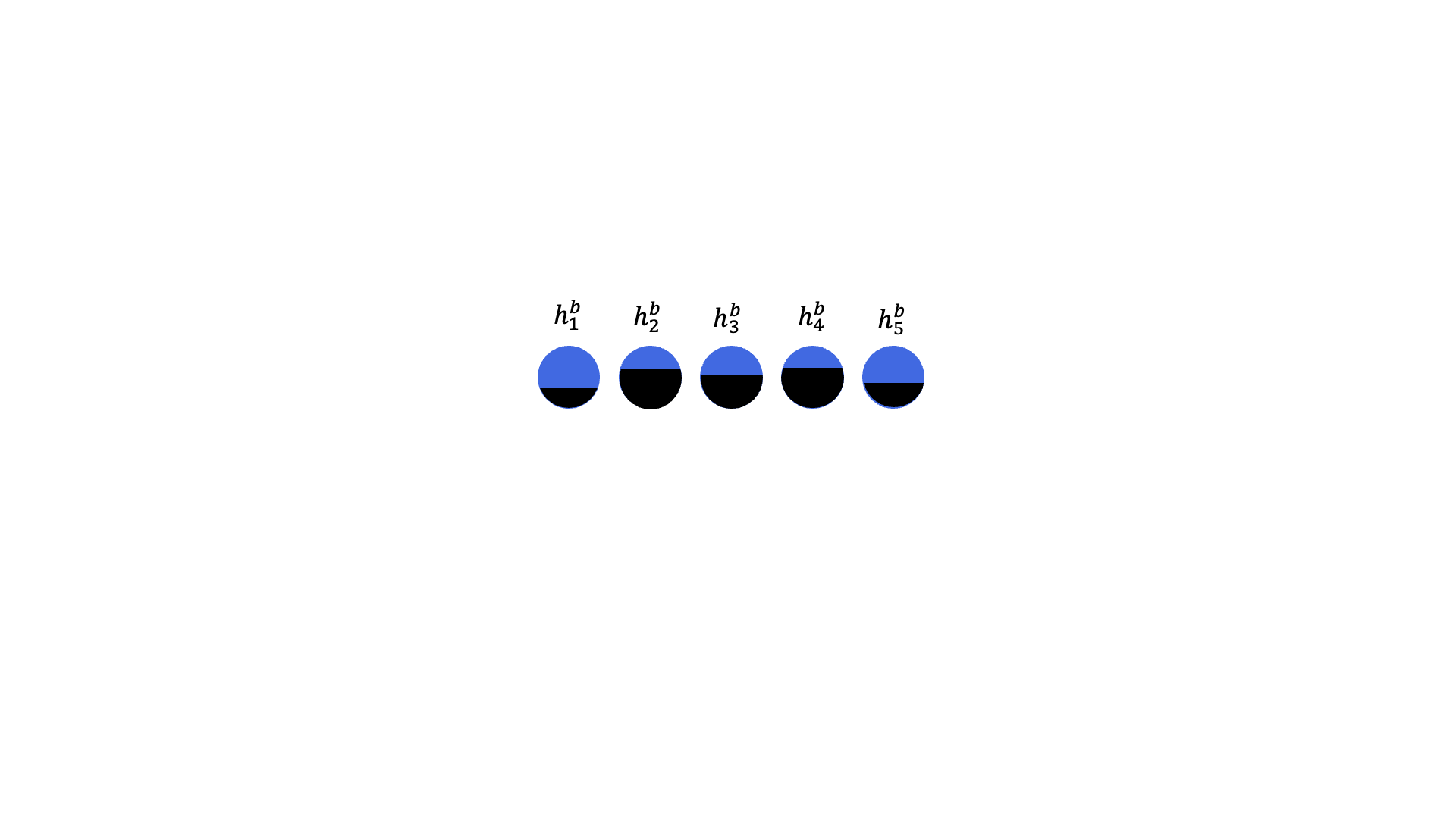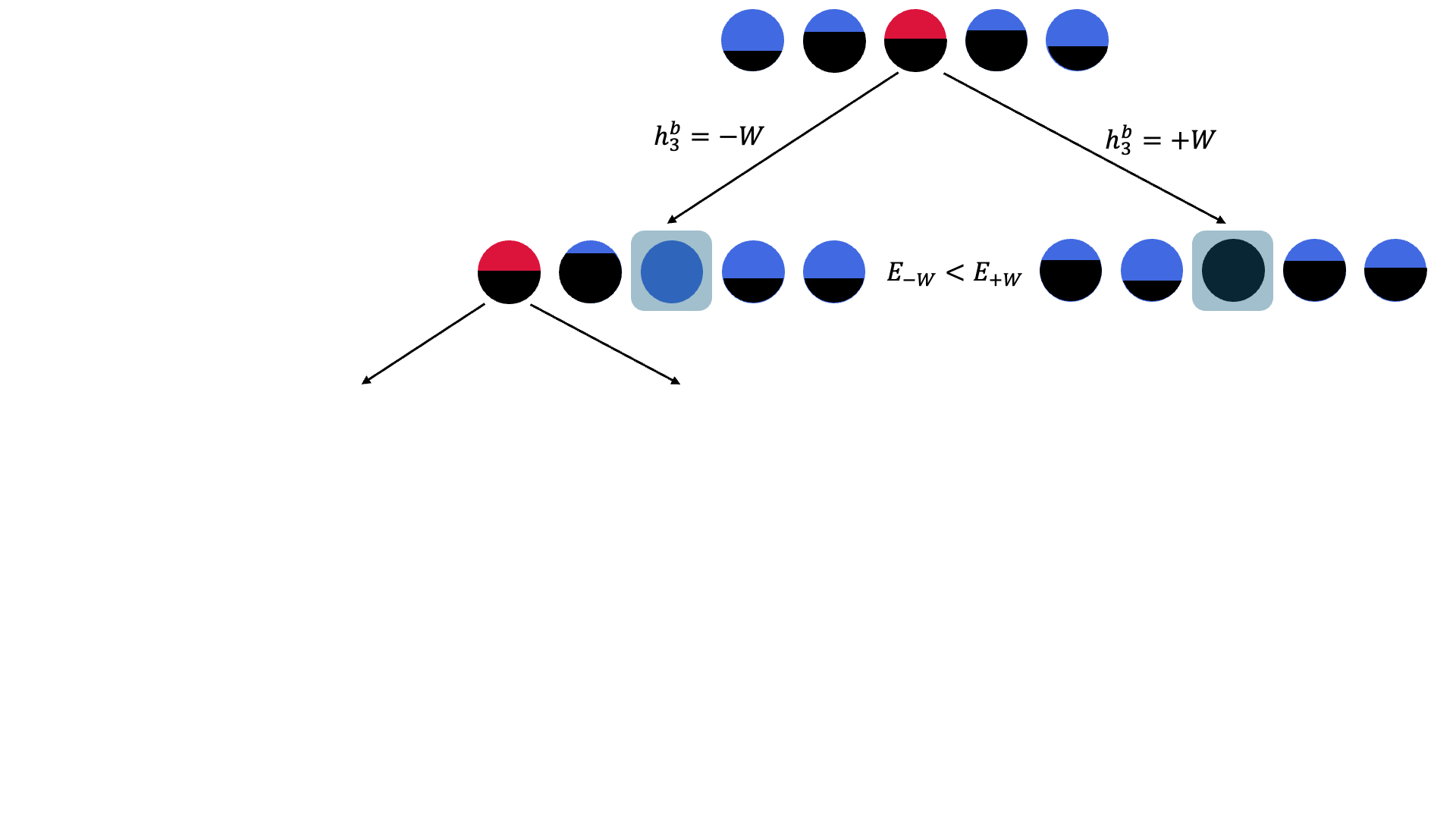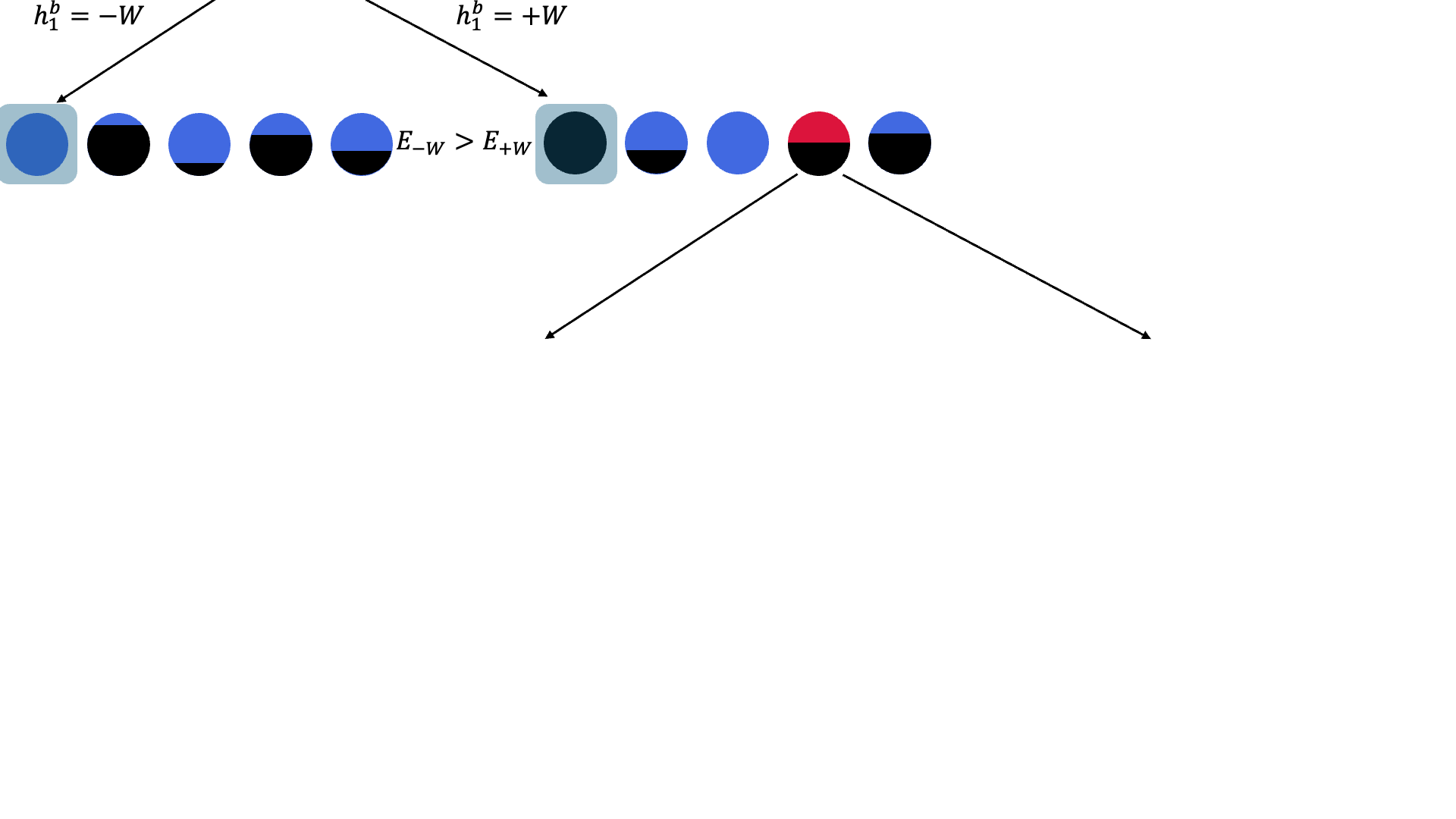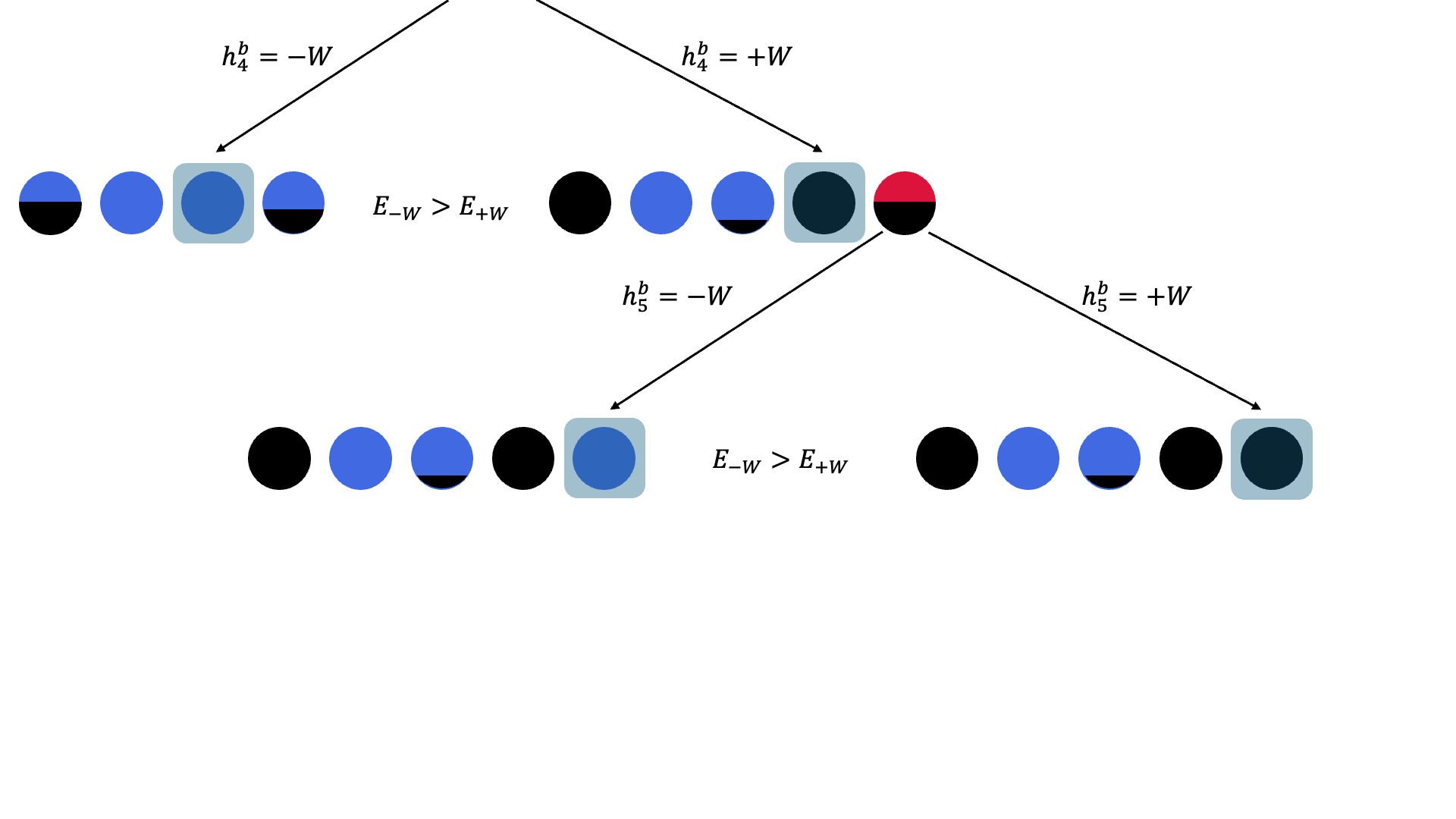Figure 1. Branch-and-bound algorithm that iteratively updates the bias fields.
Branch-and-bound digitized counterdiabatic quantum optimization
23.04.2025
As quantum hardware becomes more accessible and stable, a critical question arises: can it solve real, hard optimization problems more efficiently than classical methods? In our recent work [1], we tested a new quantum algorithm, Branch-and-Bound Digitized Counterdiabatic Quantum Optimization (BBB-DCQO) on IBM’s superconducting quantum processors to address this question directly. This new approach combines the benefits of classical well-established branch-and-bound algorithms with the efficacy and resource-efficiency of our most advanced optimization technologies: Bias-Field Digitized Counterdiabatic Quantum Optimization Algorithm (BF-DCQO) [2, 3]. The obtained results offer strong evidence that BBB-DCQO is not only practical on current quantum processors but can also outperform established classical and quantum approaches on challenging higher-order binary optimization tasks.
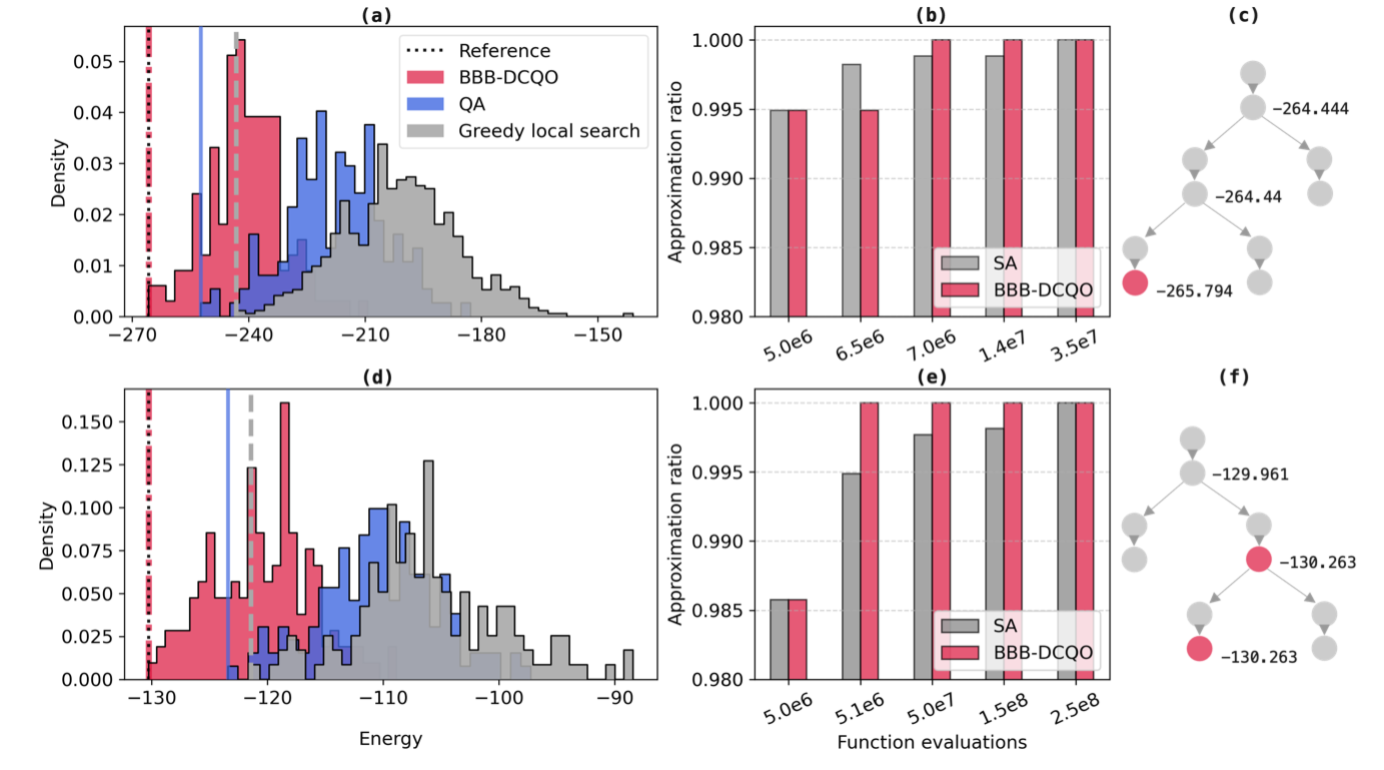
The problems we considered fall under the category of dense 100-variable HUBO (Higher-Order Unconstrained Binary Optimization) problems. These are particularly difficult because they contain both two- and three-body interactions and lack the sparsity that often makes classical approximations more effective. Moreover, mapping such problems onto quantum annealers requires introducing auxiliary variables and penalty terms, increasing the resource requirements and introducing performance trade-offs. Contrary to the approximate solutions obtained with the best D-Wave devices, BBB-DCQO reaches exact solutions on IBM quantum computers with a reduction of up to 4.2x in the required number of qubits.
We implemented BBB-DCQO on the IBM Marrakesh quantum processor using a maximum binary tree depth K=3 and executed two iterations of the BF-DCQO subroutine per branching node. Each circuit evaluation included 10,000 quantum shots, and branching was guided by expectation values to determine which spin variables were least biased. We also applied a lightweight greedy local search as post-processing to refine the low-energy samples. For a fair comparison, we benchmarked against two widely used methods: simulated annealing (SA) with a geometric cooling schedule, and quantum annealing (QA) implemented on a commercial D-Wave Advantage annealer, combined with a similar greedy post-processing step.
In both test instances, BBB-DCQO achieved the lowest-energy solutions with significantly fewer function evaluations. For the first problem, it matched the reference solution (obtained via long-run SA) using just 7 million function evaluations, compared to the 35 million used for SA. For the second problem, BBB-DCQO reached the optimal energy at the very first branching step, requiring only 5.1 million evaluations, whereas SA needed approximately 250 million evaluations to achieve the same result. This clearly indicates that optimal solutions were obtained using up to x50 less function evaluations on IBM quantum hardware. Function evaluations here include all quantum measurements, spin-flip operations in SA as warm-starting, and corrections applied during greedy local search. This metric is meaningful because it reflects the total computational effort, across both classical and quantum components, in the workflow.
Figure 2. Experimental results for two 100-qubit HUBO instances. Plots (a) and (d) show the final energy distributions for BBB-DCQO, a greedy-optimized QA and a greedy local search algorithm for both problems. The reference value is obtained from a SA with 1e8 function evaluations. Figs (b) and (e) compare the solution quality obtained from BBB-DCQO and SA with respect to the number of function evaluations. Figs (c) and (f) illustrate the convergence of the algorithm across different layers of the binary tree.
Beyond efficiency, the solution quality achieved by BBB-DCQO was consistently superior. Quantum annealing, even when enhanced with greedy correction, did not reach the same low-energy configurations. This is largely due to the difficulty of embedding dense HUBO problems into a QUBO form compatible with QA. The mapping process introduces additional variables and constraints, which distort the energy landscape and degrade performance. In contrast, BBB-DCQO operates directly on the original HUBO formulation and avoids this overhead entirely.
These results prove that BBB-DCQO is practical and scalable for accurately solving higher-order, non-convex binary optimization problems, HUBO class, on current commercial quantum processors beyond classical methods.
What’s next?
Rather than distant future, quantum computing is a present-day tool ready to tackle complex and large-scale optimization problems that are out of the reach of current classical solvers. Within a global context where industries must solve more intricate problems faster, quantum computing offers a transformative leap, unlocking novel pathways where traditional methods tend to fail. Moving from theory to actual solutions, Kipu’s mission is to continue developing the most advanced quantum algorithms capable of addressing real-world use cases, showcasing tangible benefits with current and next-generation quantum hardware. With commercial quantum advantage as a main goal, Kipu keeps pushing on designing shorter-in-depth algorithms while guaranteeing faster convergence.
References
[1] Simen, Anton, et al. Branch-and-bound digitized counterdiabatic quantum optimization
[2] Cadavid, Alejandro Gomez, et al. Phys. Rev. Research 7, L022010 (2025)
[3] IBM Quantum, Iskay Quantum Optimizer - A Qiskit Function by Kipu Quantum