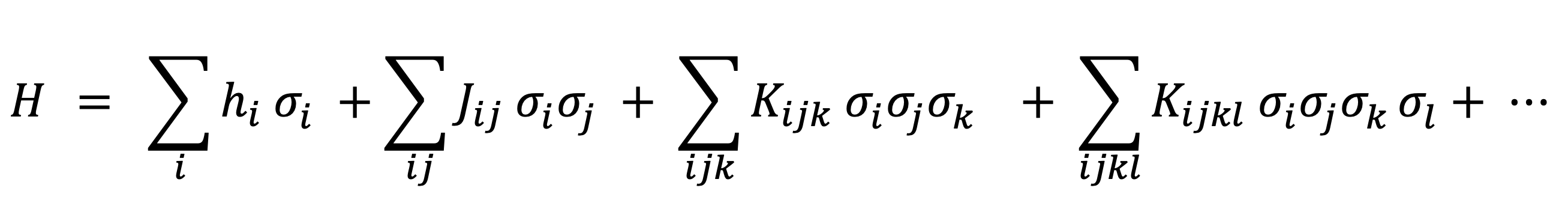Figure 1: Grid-based superconducting processors: Layout of the superconducting processor consisting of nearest neighbor qubits (red dots). Native exchange interactions of the processor can be used as analog blocks.
Digital-Analog Quantum Computing for Higher-Order problems at the Quantum Advantage level
13.05.2025
Higher-Order Binary Optimization (HUBO), Quantum Simulation of materials, and enabling Early Quantum Error Correction
We extend digital-analog counterdiabatic quantum computing (DACQC), going beyond two-body Hamiltonians, targeting higher-order Hamiltonians, to lay the groundwork in achieving quantum advantage in Higher-Order Binary Optimization (HUBO), quantum simulations and realize early quantum error correction.
The challenge of higher-order problems
Higher-order Hamiltonian based problems naturally arise in applications from finance and logistics to machine learning and quantum chemistry. Unlike second-order problems, which involve only pairwise couplings, higher-order problems can include 3-, 4-, or even higher k-body terms:
where đđ =đ,đ,đ Pauli matrices. Such Hamiltonians describe:
- Higherâorder binary optimization problems in logistics, finance, and machine learning, where multi-bit couplings capture complex cost functions;
- p-spin models in spin-glass theory and statistical physics, used to study glassy landscapes, mean-field phase transitions, and neural-networks;
- Quantum chemistry problems from correlated electron dynamics and multi-reference correlation to vibronic coupling in molecular systems, where k-body terms arise naturally in electronic structure Hamiltonians;
- Topological quantum errorâcorrecting codes such as the surface code and toric code are themselves defined by 4-body plaquette Hamiltonians on a 2D lattice, with each plaquette term enforcing local parity checks that detect and correct physical errors, laying the groundwork for fault-tolerant quantum computation.
Encoding these multi-spin interactions digitally demands deep circuits and many two-qubit gates, which rapidly become prohibitive on NISQ devices. Furthermore, the scaling increases as the number and non-locality of the higher-order terms increase.
The DACQC advantage for higher-order problems
Digital-Analog Quantum Computing (DAQC) merges the control of gate-based circuits with the native, continuous multipartite dynamics of quantum processors. By splitting a HUBO Hamiltonian into:
1. Continuous evolution under available multi-qubit interactions, and
2. Digital pulses to re-program basis and tune required coefficients we can compress the most costly, higher-order terms into short depth sequences. The result is circuits with:
- Higher fidelity per Trotter step
- Shallower overall circuit depth
These features lead to overall superior encodings suitable for NISQ processors and for early error-corrected architectures. The requirement from the quantum processor is programmable analog blocks to activate/deactivate desired couplings to realize the target Hamiltonian. This has been experimentally demonstrated by Google: see Google's nature paper. And is also available as Programmable analog block in trapped ions and in Neutral atom processors such as those demonstrated in QuEraâs Logical Qubits.
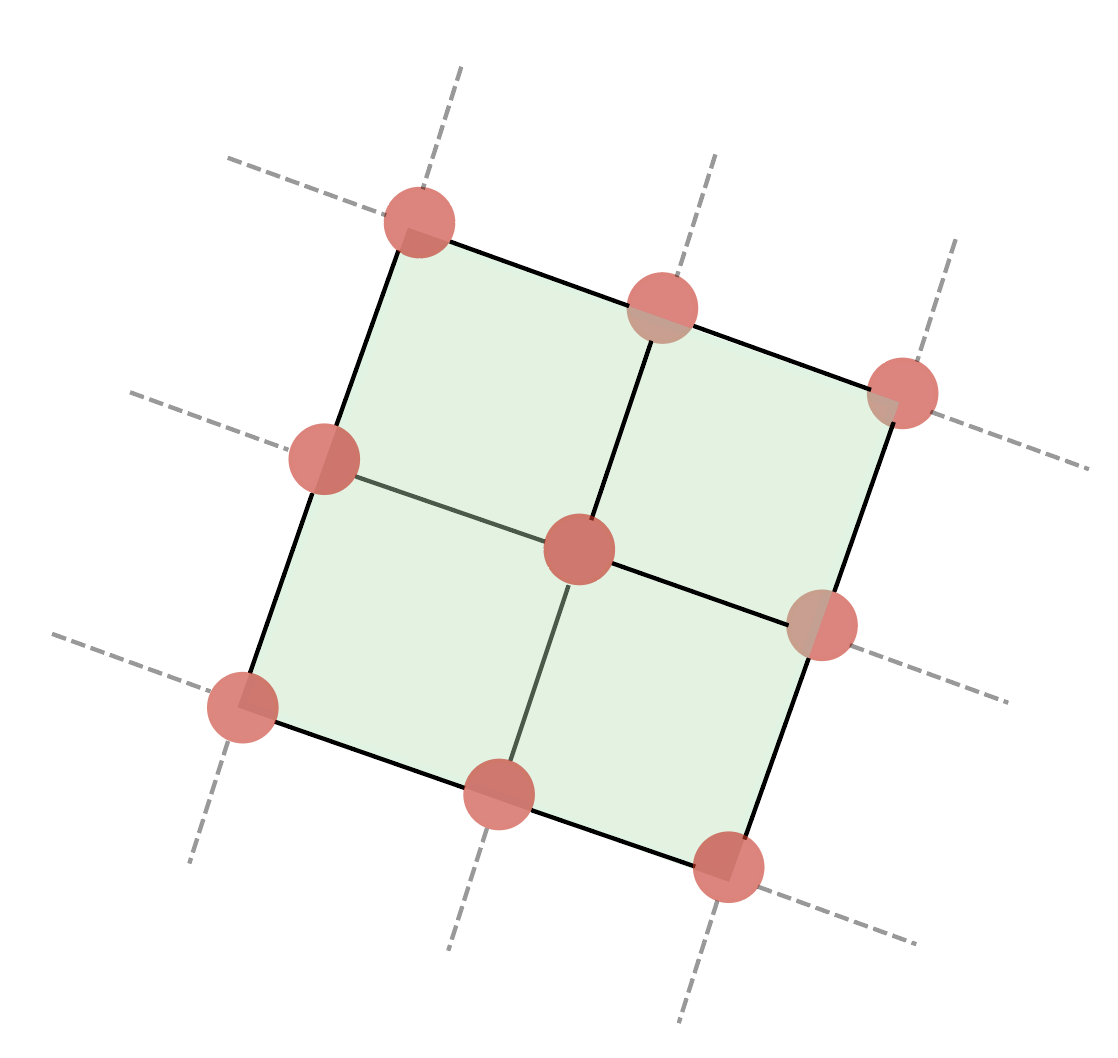
In our recent developments, we utilized superconducting processorâs exchange interaction as native analog block and achieve an encoding that can surpass pure digital encodings by a factor of 10X in the circuit depth. This is illustrated by evaluating the scaling of the encoding scheme on a 2-dimensional nĂn superconducting processor to realize all-to-all 4-body couplings (Fig. 1).
Depth scaling: from N=6 to N=102 qubits, with maximum analog block size of N/2
Circuit Depth is often the limiting resource on NISQ machines. It is an estimate of how many parallel layers of entangling gates are needed in a quantum circuit. Moreover, the number of entangling gates needed in each layer contributes to propagation of experimental errors in the hardware. For higher-order problems, the scaling of pure digital methods start to scale abruptly, due to large number of non-local terms that require deep circuits. This is exactly where the real advantage of DAQC lies, as with the long-range analog blocks, supplemented with correct digital gate operations, the protocol can realize multiple higher-order terms.
For all-to-all 4-body HUBOs, DAQC delivers dramatic depth reductions:
Performing a scaling analysis for the digital-analog decompositions, for a single Trotter step, we find that DAQC maintains one order (10-times) less scaling in the required circuit depth compared to the pure digital (Fig. 2). When run on hardware, this depth compression will not only help mitigate numerical error accumulation but also the experimental, since the required circuit fidelity falls abruptly with the gate fidelity as Fidelitym where m is the number of gates. This brings larger, more complex problems within reach of todayâs quantum devices.
Figure 2: Circuit depth scaling of digital-analog and pure digital methods: For 4-body Hamiltonians such as those described by HUBOâs and error correcting codes (Surface code, Toric code) DAQC achieves one order less scaling.
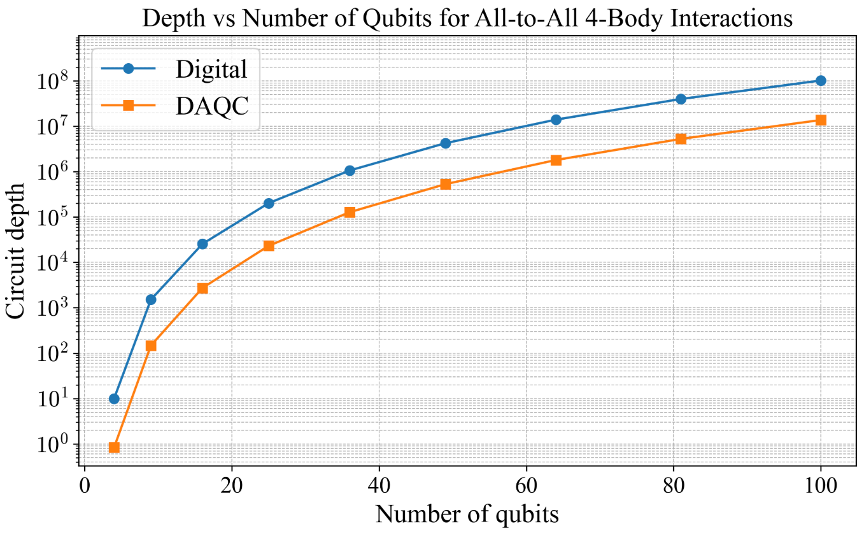
Robustness towards errors for a fixed system size
One issue that prohibits performing DAQC in the hardware is the sequential application of digital and analog pulses for a number of trotter steps, as this demands enhanced control of the analog block. Any imperfections in the analog block can propagate through the number of trotter steps required and can affect the simulation. To counteract this, we apply digital-analog counterdiabatic (CD) driving to facilitate rapid solutions, meaning to finish the algorithm in few trotter steps.
Figure 3: Comparing solution quality of DAQC and Digital methods with respect to the exact solution: Fidelity of obtaining a final ground state showcasing DAQCâs robustness towards numerical errors, achieving a much higher solution quality.
The trends of this plot (Fig. 3) from this 3Ă3 grid based superconducting processor for higher-order counterdiabatic drivings, performed with a native exchange interaction as the analog block highlight a broader point: digital-analog counterdiabatic decompositions are inherently robust in handling complex higher-order interactions.
Intuitively, a method working well on 9 qubits with many k-local interactions for a single trotter step, one expects the advantage to grow with system size. Larger systems typically have even more terms in their Hamiltonians (more pairs, more possible multi-qubit interactions), so a fully digital approach would face an explosion of gates and Trotter steps to maintain accuracy. The DAQC approach, by harnessing the analog parallelism and with CD driving, can keep the simulation manageable. For example, imagine scaling from a 3Ă3 grid to a 5Ă5 grid of qubits. The number of possible 4-body terms (like plaquettes on a lattice) increases dramatically. A digital approach would need muliple layers (depth) of gate sequences for each of these terms, dropping the fidelity unless the number of steps is increased (which then makes the circuit longer and more prone to noise). DAQC would aim to cover many of those interactions in just a few analog block sequences, preserving fidelity without a combinatorial increase in circuit depth.
This robustness is a hallmark of digital-analog methods: by using the hardwareâs natural interactions, they scale more gracefully than brute-force gate methods. It reflects a co-design philosophy â you design the algorithm with the hardwareâs strengths in mind. If your hardware can naturally do a certain two-body coupling (or a set of two-body couplings simultaneously), why not use it? The result is not only higher algorithmic fidelity but often a more scalable path to simulating bigger quantum systems. In fact, the fidelity advantage seen in the plot (DAQC vs. digital) at fixed size is likely even more pronounced if we consider increasing the number of qubits: prior studies have noted that DAQCâs edge in fidelity grows as the processor size increases as in Mitigating noise in digital and digitalâanalog quantum computation, and in DAQC with trapped ions. The digital approach tends to suffer as more qubits imply more 2-qubit gates, whereas DAQC can maintain a higher performance by using analog blocks as the quantum circuit building unit.
From a hardware implementation perspective, demonstrating that DAQC maintains high fidelity for complex interactions is a proof-of-concept that future quantum computers could be built or tuned to favor such analog blocks. It hints that hybrid control - partly analog, partly digital might be the key to unlocking quantum advantage on intermediate-scale devices and enabling early quantum error correction.
Towards practical quantum advantage and early quantum error correction
Key takeaways for higher-order problems:
- Digital-Analog evolution blocks natively synthesize k-body couplings and syndrome-extraction operators, bypassing deep gate decompositions.
- Gate count and runtime drop by 10X in benchmark higher-order problems such as HUBOs and error correcting code, collapsing circuit-depth overhead from O(N2k) to O(Nk+1)
- Depth compression not only mitigates Trotter error but also suppresses coherent and stochastic noise accumulationâenabling early demonstrations of quantum error correction (e.g. small-scale surface-code syndrome extraction) on NISQ hardware.
This hybrid DAQC paradigm therefore unlocks both larger HUBO problem sizes and the building blocks of early quantum error correction.
A call to hardware providers
Despite these compelling results, DAQC remains under-leveraged by many quantum-hardware companies. Programmable platformsâfrom superconducting qubits (Google, Rigetti, IQM) to trapped ions (AQT, eleQtron), neutral atoms (QuEra, Pasqal), and photonics (Quandela)âalready possess analog resources for multi-spin evolution:
- Superconducting resonator couplings can natively drive 4-body plaquette terms.
- Global multimode ion drives can realize long-range k-spin interactions.
- Rydberg blockade graphs support higher-order couplings in atom arrays.
By integrating DAQC tools-compact analog pulses complimented with digital controls, hardware vendors can demonstrate near-term quantum advantage on quantum optimization and simulation.
Looking ahead at Kipu Quantum
At Kipu, weâre pushing DAQC forward to solve problems in the following fields:
- Material simulations (e.g., extended Hubbard and Holstein models);
- Quantum chemistry of strongly correlated molecules;
- Complex HUBO optimizations in logistics, finance, and ML;
- Early quantum error correction
Our benchmarks using existing Kipu quantum algorithms already outperform classical solvers (tensor networks, Gurobi, CPLEX) on mid-size instances Bias-field DCQO for HUBO's. We invite hardware partners to collaborate on DAQC-driven demonstrations of quantum advantage in the coming months.