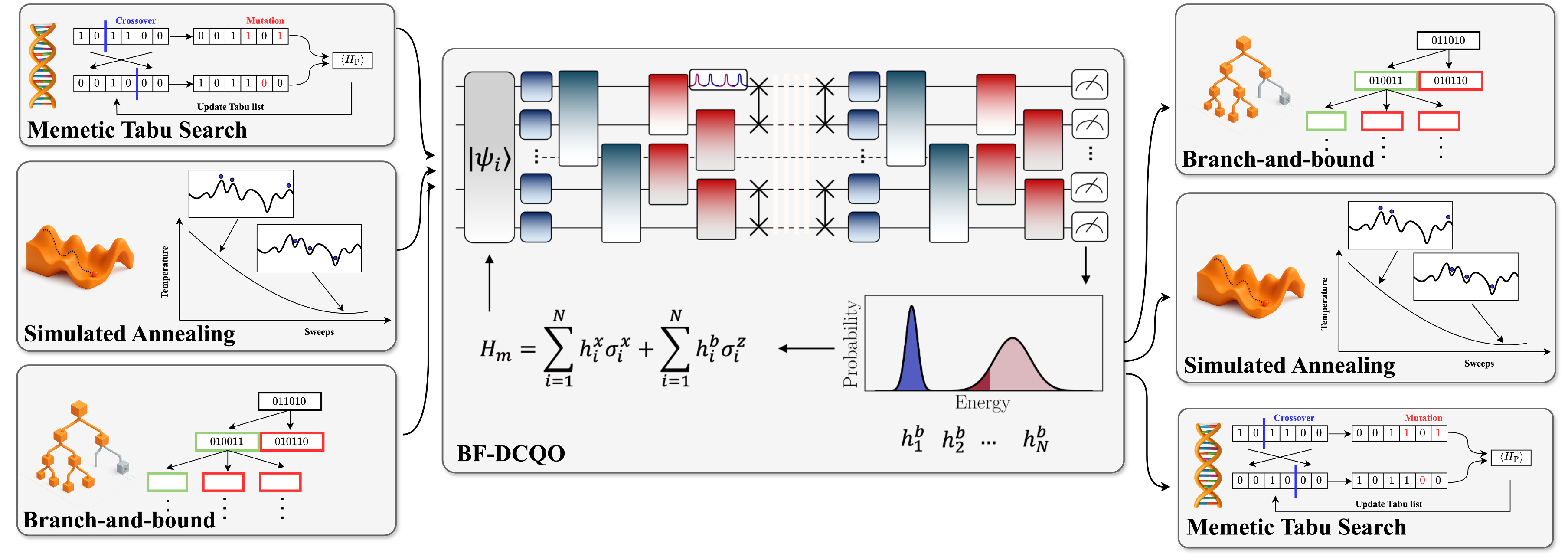
Hybrid Sequential Quantum Computing

09.10.2025

Combinatorial optimization lies at the core of many industrial and scientific problems, from logistics and energy grids to finance, manufacturing, and materials design. Yet, as problem sizes increase, classical methods such as simulated annealing (SA), memetic tabu search (MTS), or exact solvers like CPLEX face steep scalability barriers.
 
At Kipu Quantum, we explore a new way forward: non-trivial sequencing of classical and quantum optimization routines that yield measurable speedups at the runtime quantum-advantage level. Built upon Sequential Quantum Computing paradigm [1], this approach, introduced in our latest study 'Hybrid Sequential Quantum Computing (HSQC)' [2], demonstrates how carefully ordered computational stages can redefine runtime efficiency on today’s quantum processors.

Rethinking Hybridization: From Mixing to Orchestration

Many hybrid algorithms alternate between quantum and classical phases in fixed feedback loops. HSQC instead focuses on runtime-adaptive sequencing, where each stage is deliberately positioned to exploit its specific computational strength and mitigate the weaknesses of the others.
 
This composition is not trivial: the order, duration, and transfer of information between stages directly determine the achieved performance. One of the workflow examples proceeds as follows:

1. Classical exploration (SA): efficiently maps the energy landscape to identify promising low-energy configurations.
2. Quantum refinement (BF-DCQO) [3,4]: leverages digitized counterdiabatic quantum evolution and discovers deeper minima.
3. Classical exploitation (MTS or SA): refines the quantum-enhanced solutions locally, steering the system toward the ground state.

Hybrid sequential quantum computing (HSQC) schematic. The HSQC framework tested begins with a classical optimizer to find promising low-energy states, then seeds the BF-DCQO protocol on a QPU. The digitized counterdiabatic quantum evolution to escape to deeper minima, after which a final classical pass refines the obtained solutions to the ground state.

Runtime Quantum-Advantage Level in Action

We validated this sequential orchestration on dense higher-order unconstrained binary optimization (HUBO) problems executed on IBM’s 156-qubit heavy-hex superconducting processors. Two runtime pipelines were tested:

• SA → BF-DCQO → MTS, combining stochastic sampling, counterdiabaticity, and memetic local search.
• SA → BF-DCQO → SA, where quantum outputs continue to a second simulated annealing process.

Across all instances, sequential orchestration consistently surpassed standalone classical solvers. For the best-case instance:

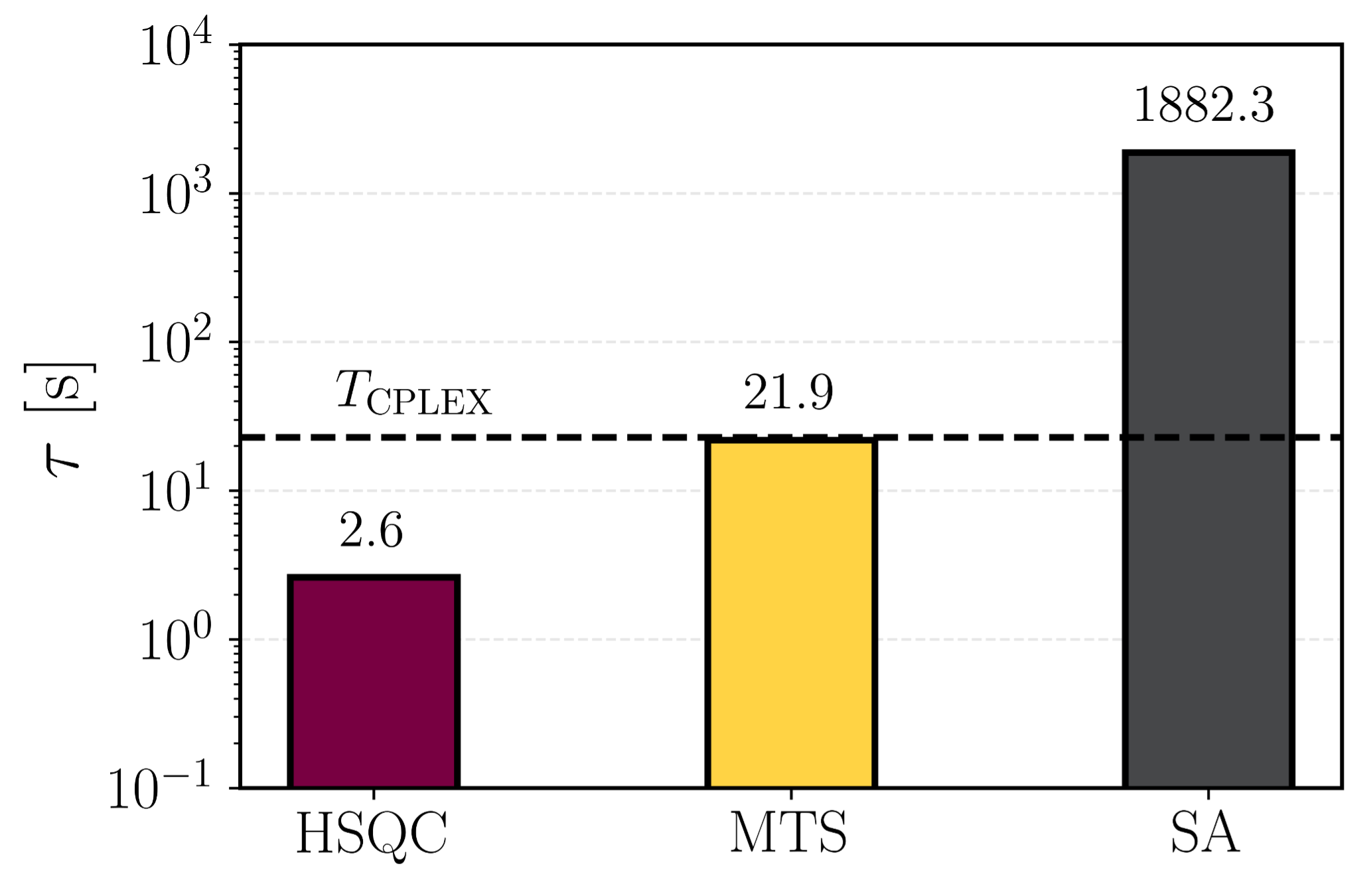
• HSQC reached the ground state in estimated ~3 seconds,
• compared to estimated ~22 seconds for MTS and estimated ~1800 seconds for SA, achieving up to 700× faster convergence over SA and 9× faster over MTS.

The runtime quantum-advantage level is clear: HSQC matches or exceeds the solution quality of exact solvers like CPLEX (≈ 23 s per instance) while operating an order of magnitude faster.

N = 156, 2 SWAP layers, problem instance has 125 two-body terms and 616 three-body terms. HSQC achieves solutions nearly up to ~700× faster than simulated annealing (SA), ~10× faster than memetic tabu search (MTS) and CPLEX.

Why Sequential Order Matters

The advantage stems from the selective interplay between computational paradigms.

• During the BF-DCQO stage, bias-field feedback transforms measurement statistics into adaptive guidance for the next classical phase.
• The MTS refinement then exploits this structure, combining evolutionary exploration with tabu-guided local search to avoid retracing previous minima.
• Runtime allocation between these stages is adaptive, optimizing efficiency based on the observed energy landscape

Performance comparison between MTS/SA and HSQC. (a) For different numbers of generations, G_max, optimality gaps 𝒢 obtained across the eight instances tested. Data points lying in the lower part of the plot mean that the HSQC approach performed better than MTS. (b) For different numbers of sweeps, optimality gaps were obtained across the same eight instances. Here, 𝒢 =100(E_min-GS)/|GS|

Comparing with Other Quantum Strategies

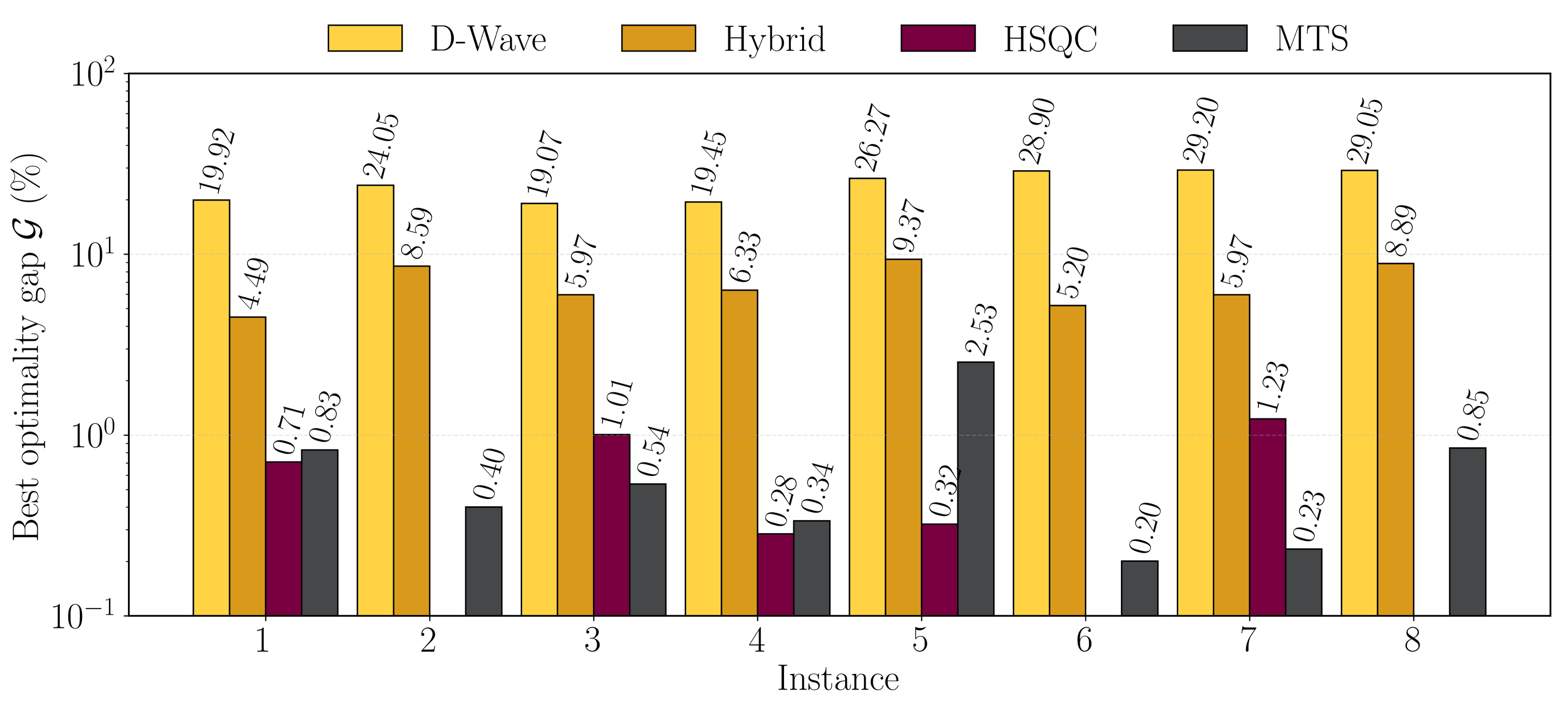
To contextualize HSQC’s results, we benchmarked against D-Wave’s Advantage2_system1.6 annealer and their hybrid solvers up to 4 seconds of time limit computation. Even with long annealing times ranging from 0.5 µs up to 2000 µs and additional classical post-processing, D-Wave solutions displayed 20–35% optimality gaps relative to the ground state, with a total QPU sampling time ranging from 5.5-9.5 s on average. In contrast, HSQC’s non-trivial sequencing achieved near-optimal or exact solutions on IBM’s digital quantum processors without the overhead of HUBO-to-QUBO mapping or auxiliary qubits required for posterior embedding. Much faster and better solutions were obtained with HSQC using 10x fewer qubits than D-Wave. These results highlight how quantum annealers are not well-suited for higher-order optimization, whose qubit overhead worsens with increasing problem density and k-locality of the many-body terms, and undermines the quality of the solutions and scalability.

Performance comparison between D-wave Advantage, D-wave Hybrid-solver, HSQC and MTS. Minimum optimality gaps G obtained across the eight instances tested. Here, G=100(E_min-"GS" )\/|"GS" |, meaning the lower the gap the better. Omitted bars indicate that the ground state energy was reached.

Towards Runtime-Optimized Quantum Workflows

Sequential quantum optimization is more than an algorithmic design. It represents a modular and evolving workflow in which each stage can be independently upgraded as quantum hardware, heuristics, or compilation strategies advance. This modularity ensures scalability toward larger HUBO instances and compatibility with next-generation processors — in step with the rapidly accelerating roadmaps of quantum hardware providers, where qubit counts, connectivity, and chip architectures are improving at record pace.
 
Future directions include deploying this sequencing framework on two-dimensional architectures with enhanced connectivity, and integrating a generative-AI agent capable of autonomously designing and orchestrating classical–quantum execution sequences in real time. Such an adaptive agent would learn from performance feedback, dynamically optimizing runtime allocation and stage ordering.
 
These developments mark a decisive step toward quantum advantage in optimization, turning experimental research into real-world applications across logistics, manufacturing, and telecom.

References

1. Romero, S. V. et al. ‘Sequential Quantum Computing’, arXiv:2506.20655 (2025).
2. Chandarana P. et al., 'Hybrid Sequential Quantum Computing', arXiv:2510.05851 (2025).
3. Chandarana P. et al., 'Runtime Quantum Advantage with Digital Quantum Optimization', arXiv:2505.08663 (2025).
4. Cadavid A. G. et al., 'Bias-Field Digitized Counterdiabatic Quantum Optimization', Phys. Rev. Res. 7, L022010 (2025).