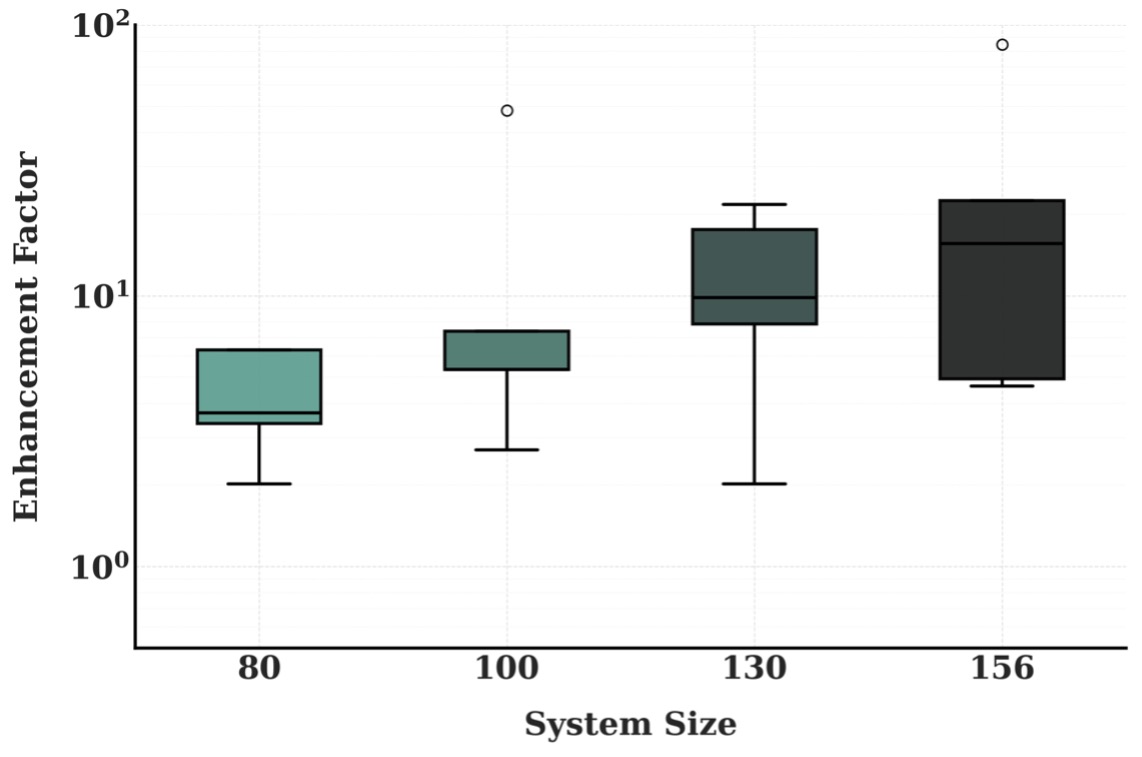
Figure 1. Enhancement factor, meaning ratio of CPLEX runtime to BF-DCQO runtime, as a function of system size or number of qubits. Each box summarizes results across multiple problem instances; the line inside shows the median, the box covers the middle 50% of data, and dots indicate outliers—cases with exceptionally high speed-up.
Runtime Quantum Advantage with BF-DCQO
25.04.2025
In the challenging domain of combinatorial optimization, higher-order unconstrained binary optimization (HUBO) problems are renowned for their computational complexity. Classical solvers like CPLEX and simulated annealing (SA) often struggle with severe runtime bottlenecks when higher-order terms come into play, exponentially increasing computational demands and limiting scalability.
Our team set out to precisely explore this unfriendly territory. At Kipu Quantum, we have introduced Bias-Field Digitized Counterdiabatic Quantum Optimization (BF-DCQO), a transformational quantum algorithm tailored specifically for tackling complex optimization problems. BF-DCQO combines well-established counterdiabatic quantum dynamics protocols with a clever measurement-driven bias-update strategy, efficiently navigating complex energy landscapes where classical solvers typically stumble. We deployed BF-DCQO on IBM’s latest 156-qubit Heron machines and benchmarked the time required to produce high-quality solutions.
The results are impressive: BF-DCQO is able to consistently achieve comparable quality in the yielded solutions for the tested instances up to 80 times faster than CPLEX, or up to 12 times faster than SA. This occurs despite the quantum chip’s modest shot rate (~10 kHz) compared to classical hardware, which evaluates around 10^8 samples per second. Moreover, the performance gap grows as the system size increases, clearly indicating that we are trespassing quantum-advantage level for wide classes of combinatorial optimization problems as compared to the tested solvers. This experimental achievement of Kipu Quantum algorithms running in commercial quantum processors, in absence of sophisticated error mitigation, error correction, or fault-tolerant encodings, proves that utility scale and quantum-advantage level in quantum computing is possible today, even with noisy qubits. We can easily imagine that, when error-corrected or fault-tolerant quantum computers may start to be available in the future, Kipu Quantum algorithmic solutions will show even more powerful results on logical qubits. Given the ambitious roadmaps and reliability of most quantum hardware providers, we consider that systematic quantum advantage will naturally happen and consolidate along this year 2025.
Quantum vs. Classical: Performance Benchmarks
To rigorously validate BF-DCQO, we performed extensive benchmarks on the ibm marrakesh backend, which features 156 transmon qubits arranged in a heavy-hex architectural lattice. We tested our quantum algorithm on dense HUBO problems involving up to three-body terms and coefficients drawn from heavy-tailed distributions. The chosen coefficients closely mirror real-world optimization problems encountered in wide classes of use cases in finance, risk management, and regulatory compliance. Similar cases can be developed for logistics, manufacturing, telecommunications networks, energy distribution, robotics, chemistry, navigation, and life sciences.
Fig.1 shows how fast our BF-DCQO is, as compared to CPLEX across different system sizes or number of qubits [1]. As this size increases, we see that not only does the average improvement grow, but the potential for dramatic speed-ups becomes even more pronounced. We can clearly see that for some instances the runtime improvements are modest, while for most of them, drastic enhancements happen.
Figure 2. Accuracy of simulated annealing (SA) and BF-DCQO across two instances corresponding to two system sizes with 130 and 156 qubits.
Figure 3. Runtime to find 99.8% of the optimal solution for an N=156 qubit instance using BF-DCQO, CPLEX, and SA.
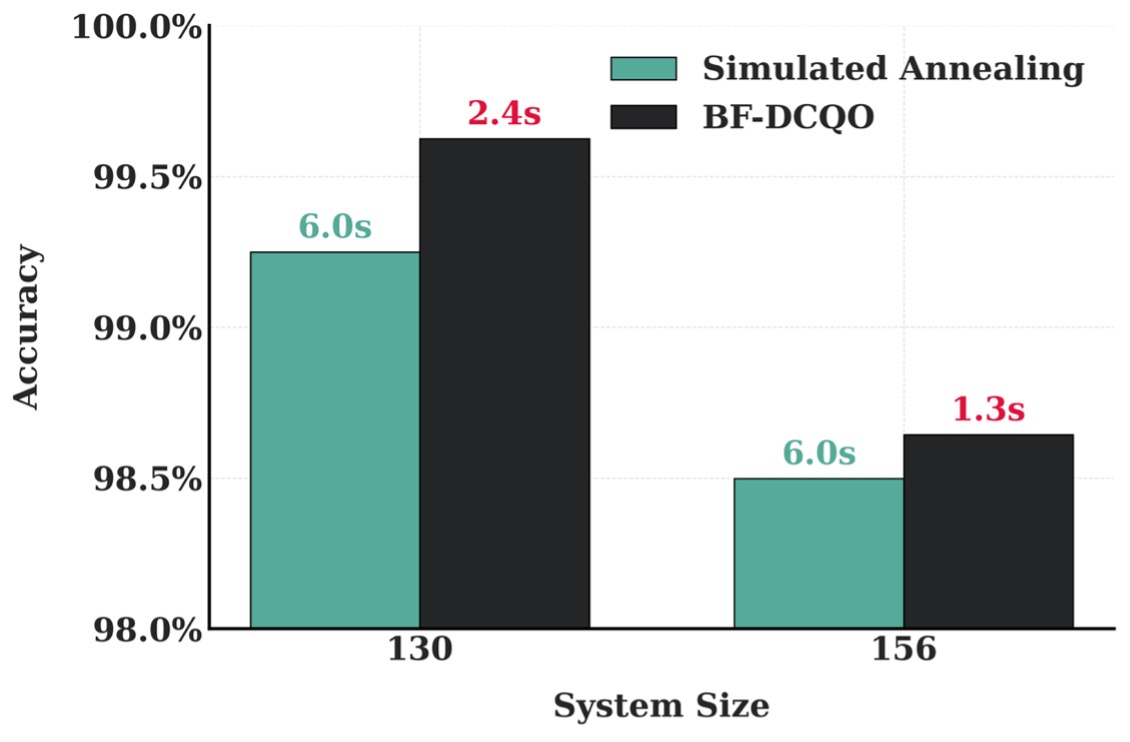
On the other hand, Fig. 2 demonstrates how BF-DCQO outperforms SA in both accuracy and runtime. For both methods, accuracy is evaluated relative to the optimal solution. Although SA achieves near-optimal accuracy, BF-DCQO consistently delivers superior results, particularly for the larger problem instance. Execution times in seconds are annotated above each bar, highlighting BF-DCQO’s faster convergence, achieved even with comparable or better accuracy. Notably, SA requires exploring at least four orders of magnitude more samples than BF-DCQO to reach similar accuracy.
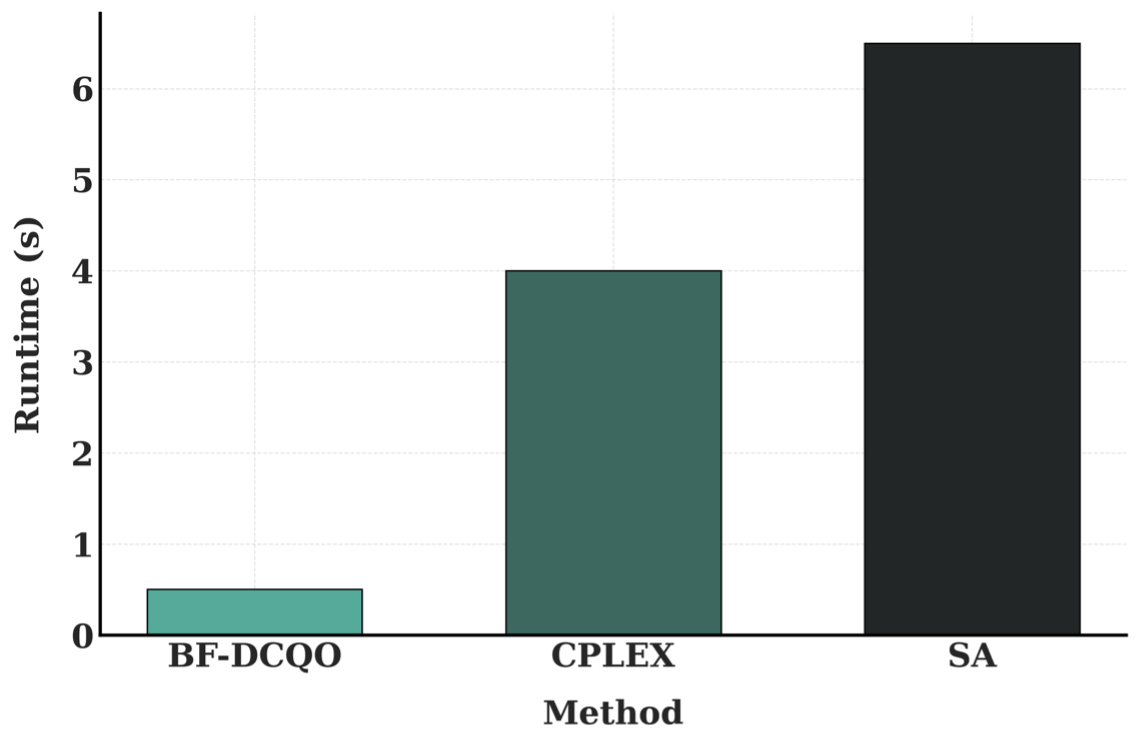
Both Fig. 1 and Fig. 2 clearly illustrate that BF-DCQO's performance advantage grows significantly with system size. In larger scenarios, such as the 100- and 156-qubit cases, we observe speed-ups exceeding an order of magnitude. Also, in Fig. 3, we show results for simultaneously outperforming both CPLEX and SA for a 156-qubit instance. The takeaway is clear: the larger the optimization problem, the greater the advantage of BF-DCQO, showing signatures of scaling quantum advantage.
Decoding Runtime Quantum Advantage
BF-DCQO’s superior performance is rooted in four key design principles:
- Digitized Counterdiabatic Protocol: By minimizing unwanted excitations among energy levels during rapid counterdiabatic quantum evolution, BF-DCQO, its digitized counterpart, significantly increases the probability of obtaining optimal or near-optimal solutions.
- Measurement-driven Bias Updates: BF-DCQO leverages measurement information from each DCQO iteration to adaptively navigate complex energy landscapes, resulting in faster convergence.
- Nonvariational Quantum Algorithmics: our BF-DCQO is in essence and by construction an iterative purely quantum algorithm without any drawback coming from others’ variational approaches.
- Native Embedding of Complex Interactions: Classical solvers like CPLEX typically decompose higher-order terms into large sets of linear constraints and additional binary variables, introducing substantial computational overhead. Although SA can directly tackle HUBO problems, it often struggles since it gets stuck in local minima within rugged energy landscapes. In contrast, BF-DCQO can efficiently handle higher-order terms, providing an encoding advantage, significantly improving the speed of convergence and the quality of the solution.
Quantum Advantage and the Path to Commercial Realization
Our success with BF-DCQO represents a significant milestone, clearly demonstrating superior speed and accuracy compared to advanced classical solvers. Today's quantum processors already enable remarkable algorithmic performance. However, upcoming quantum platforms, such as IBM’s 1000+ qubit "Flamingo" systems will further enhance BF-DCQO’s capabilities, promising substantial breakthroughs in solving previously intractable optimization problems. Quantum algorithms like BF-DCQO will soon tackle even denser HUBO problems that are challenging for classical computations, firmly consolidating and establishing the era of commercial quantum advantage. We actively welcome collaborations and partnerships with industry leaders and top researchers to accelerate together the exciting present and future of quantum optimization.
[1] We thank Stefan Woerner from IBM for sharing his expertise on using CPLEX through private communication and for his valuable feedback.