Figure 1. Sequential quantum computing schematic. Different quantum hardware architectures offer distinct advantages. SQC integrates homogeneous and heterogeneous quantum processors, combining their strengths and addressing their limitations to enhance solution quality while minimizing resource utilization.
Sequential Quantum Computing
Integrating multiple quantum processors for better solutions
30.06.2025
Today’s quantum landscape offers a range of processors, each with unique strengths and limitations. But can we harness the best of every device? At Kipu, we’ve pioneered Sequential Quantum Computing (SQC) [1]: a paradigm that links different quantum processors in series to overcome individual bottlenecks and unlock advanced capabilities on today’s hardware.
How does SQC work?
Similar to the preparation of a gourmet dish, where sourcing each ingredient from specialized shops is preferred over a single supermarket with average-quality items, SQC employs a sequential workflow, utilizing different quantum processors to acquire higher-quality solutions.
Individually, digital and analog quantum processors offer distinct advantages but also specific constraints. SQC mitigates individual limitations by sequentially transferring information between commercial quantum processors, creating seamless quantum algorithmics that enhance the performance of the targeted tasks.
We announce the launch of a diverse range of quantum computing solutions, encompassing both sequential and parallel, classical and quantum, as well as homogeneous and heterogeneous quantum processing workflows. This novel SQC paradigm will provide enhanced performance and earlier quantum advantage for industry applications as quantum computers evolve from noisy to error-corrected to fault-tolerant quantum devices.
Experimental Breakthrough
The promise of SQC is not just theoretical or conceptual. We have already demonstrated its potential by addressing a combinatorial optimization problem with interactions involving hundreds of three-body terms. We considered a 156-qubit problem adapted to IBM Heron devices up to three-body terms with randomly chosen Sidon set couplings. These are known to yield non-degenerate landscapes [2]. For such a task, our bias-field digitized counterdiabatic quantum optimization (BF-DCQO) algorithm was used, since it has proven superior performance on digital platforms [3, 4, 5, 6]. It turns out that within the SQC paradigm, BF-DCQO is also a suitable quantum algorithm if the state initialization utilizes quantum annealing (QA) for computing the biases. Along these lines, for the sake of a balanced benchmarking, three approaches are considered:
- Standalone QA (D-Wave): Hundreds of thousands of measurements.
- Standalone BF-DCQO (IBM): Ten iterations with tens of thousands of measurements.
- SQC (D-Wave+IBM): one iteration of BF-DCQO on IBM with five thousand shots, warm-started with a solution from QA with three thousand samples. Therefore, the overall routine required fewer than ten thousand shots.
The logic behind this combination is to obtain fast, high-quality results from D-Wave as a warm start of a BF-DCQO algorithm run on IBM. Digital quantum processors admit the computation of nonstoquastic terms, which can yield better results as an outcome. In consequence, not only were the obtained solutions better, but they also required fewer resources, showcasing a clear advantage of sequentially combining both quantum processors (see Table 1). In particular, the significant reduction in the number of required measurements was 36x for QA and 6x for BF-DCQO.
| Approach | Number of shots | AR | Best AR | Best energy | Qubits |
|---|---|---|---|---|---|
| Standalone QA (large) | 290000 (26.1 s) | 96.63% | 98.89% | -184.78 | 678 |
| Standalone BF-DCQO | 50000 (5.0 s) | 90.10% | 97.52% | -182.21 | 156 |
| Standalone QA (low) | 3000 (0.6 s) | 90.70% | 98.51% | -184.07 | 678 |
| SQC | 8000 (1.1 s) | 94.95% | 100% | -186.86 | 678/156 |
Figure 2. Results for the heavy-hexagonal 156-qubit NN HUBO. (a) Using D-Wave, post-processed distributions using 290000 and 3000 samples (dark blue and lavender, respectively) and annealing time of 90 μs. Using IBM, best post-processed distribution after ten iterations of BF-DCQO (purple). Using both D-Wave and IBM (SQC approach, yellow), one iteration of BF-DCQO after initializing the bias fields with the post-processed D-Wave distribution of 3000 samples. (b)-(c) Approximation ratios and best approximation ratios obtained.
Stability
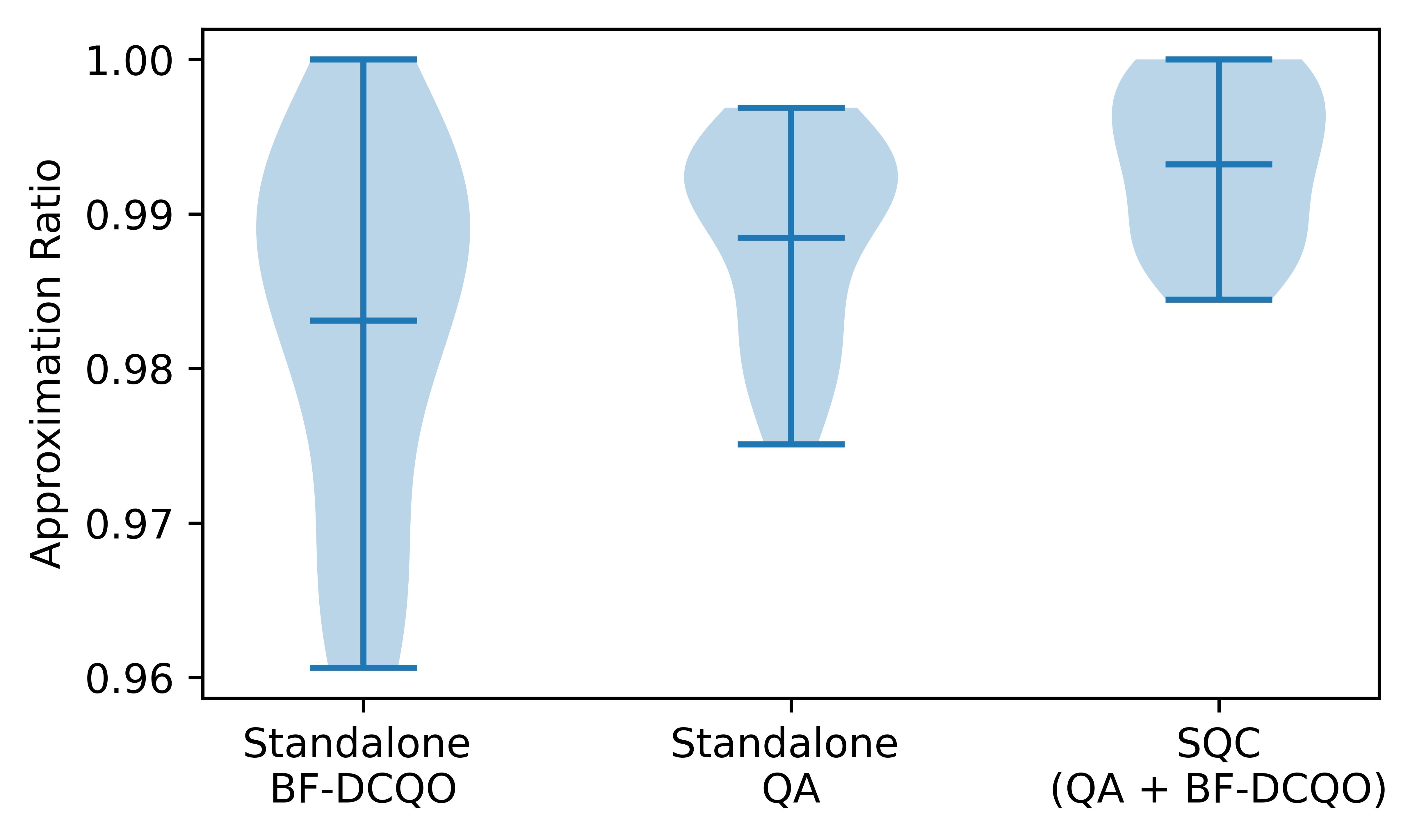
To evaluate performance across multiple instances, we considered 17 randomly distributed Sidon instances, as described above. Then, we compared the following three methods:
- Standalone QA (D-Wave) with 50K measurements.
- Standalone BF-DCQO (IBM) with 5 iterations and 10K measurements per iteration.
- SQC (D-Wave+IBM) with 4K QA shots and 3 IBM iterations with 10K measurements.
In Fig. 3, we show the distribution of approximation ratios for these three methods. We observed that the combined SQC approach performed better on average than the individual workflow. Furthermore, the spread of the data was smaller. This indicates that there are a significant number of cases where SQC offers advantages.
Figure 3. Approximation ratio distribution over the studied instances for the three methods: BF-DCQO on digital IBM, QA on analog D-Wave, and the combination of both as a SQC approach.
Why SQC matters
SQC represents a powerful and versatile approach to addressing computational challenges that the currently evolving quantum hardware struggles with. The ability of the SQC paradigm to integrate different quantum platforms promises significant advancements in performance and efficiency. SQC is not limited to optimization problems. In fact, it has a broader applicability. Future efforts will focus on expanding SQC to domains such as quantum simulation of materials, quantum chemistry, and quantum machine learning, paving the way for more groundbreaking discoveries.
Sequential quantum computing is more than just a technological innovation: it is a leap forward in quantum science and commercial quantum computing under realistic conditions. By combining the strengths of various quantum processors, SQC opens up new possibilities for solving complex problems efficiently while pushing the boundaries of what current quantum hardware can achieve separately. Whether it is quantum chemistry, materials science, quantum artificial intelligence, or large-scale optimization challenges, SQC is poised to reshape the landscape of computational research.
References
- Romero SV, Cadavid AG, Solano E, Hegade NN. Sequential Quantum Computing. arXiv preprint arXiv:2506.20655 (2025) .
- Katzgraber HG, Hamze F, Zhu Z, Ochoa AJ, Munoz-Bauza H. Seeking Quantum Speedup Through Spin Glasses: The Good, the Bad, and the Ugly. Phys. Rev. X. 5:031026. 2015 Sep 1.
- Cadavid AG, Dalal A, Simen A, Solano E, Hegade NN. Bias-field Digitized Counterdiabatic Quantum Optimization. Phys. Rev. Research 7:L022010. 2025 Apr 9.
- Romero SV, Visuri AM, Cadavid AG, Solano E, Hegade NN. Bias-Field Digitized Counterdiabatic Quantum Algorithm for Higher-Order Binary Optimization. arXiv preprint arXiv:2409.04477. 2024 Sep 5.
- Simen A, Romero SV, Cadavid AG, Solano E, Hegade NN. Branch-and-bound Digitized Counterdiabatic Quantum Optimization. arXiv preprint arXiv:2504.15367. 2025 Apr 21.
- Chandarana P, Cadavid AG, Romero SV, Simen A, Solano E, Hegade NN. Runtime Quantum Advantage with Digital Quantum Optimization. arXiv preprint arXiv:2505.08663. 2025 May 13.