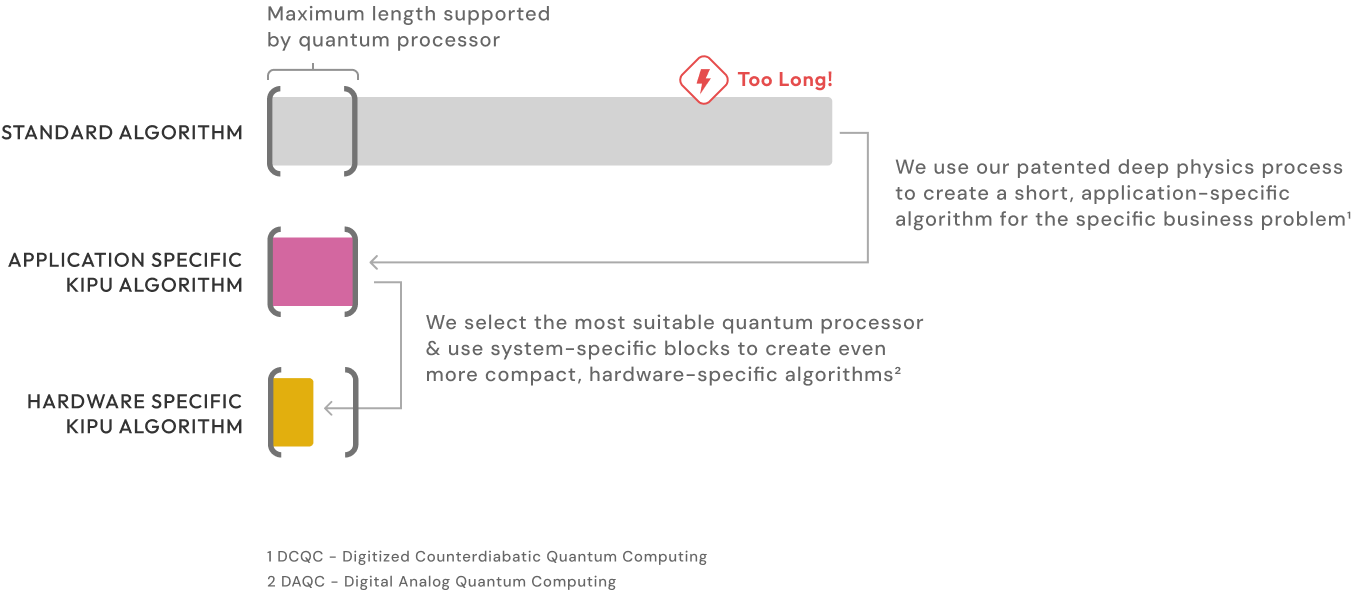
Application- and hardware-specific quantum computing solutions

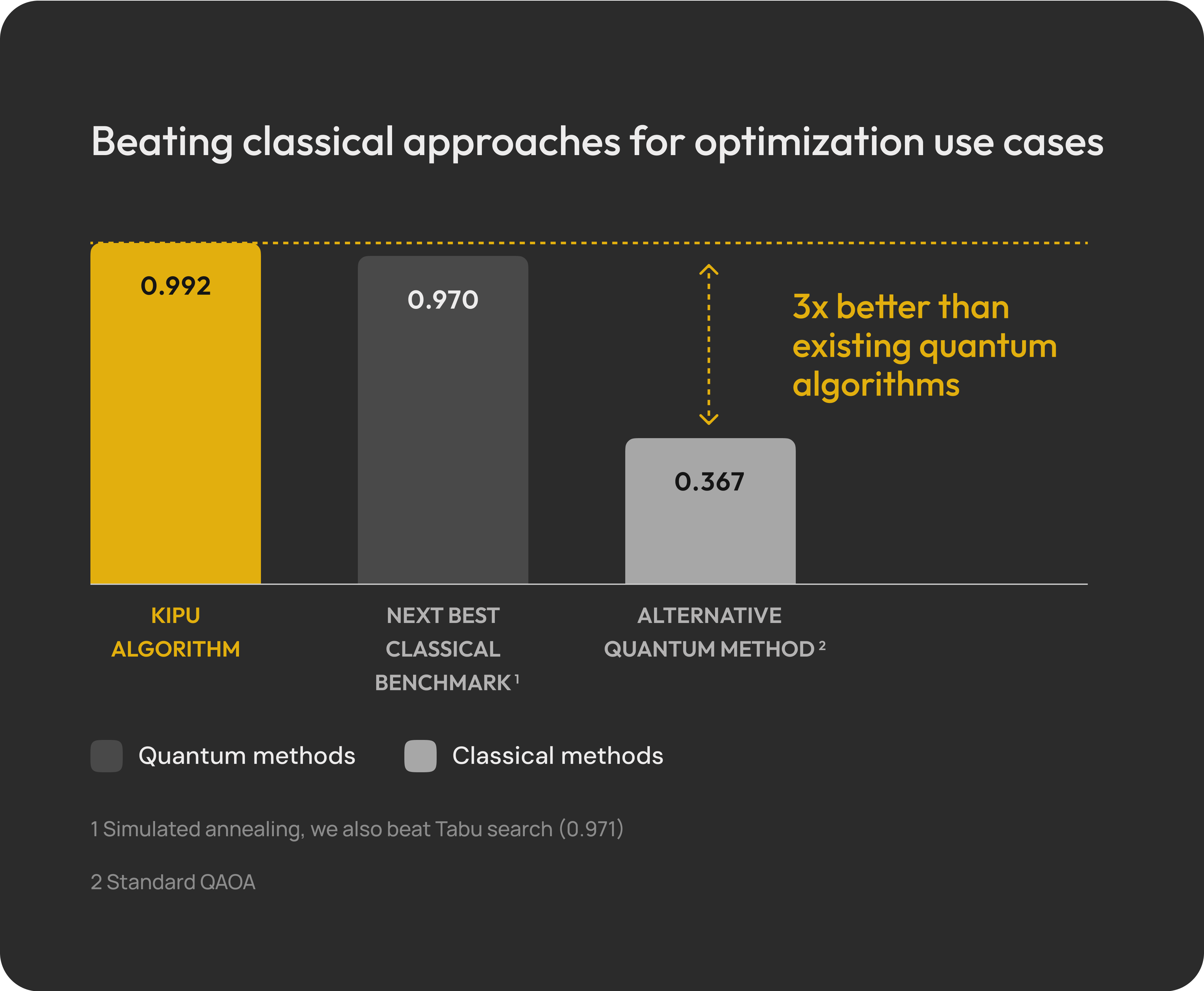
HUBO (higher order unconstrained binary optimization problem) solves real-world problems.
HUBO is more complex but more practically relevant than QUBO mapping. HUBO allows tackling of more realistic, complexer problems with continuous variables. Great for protein folding, scheduling, financial modeling, mixed-integer optimization.